O controle PID é a ferramenta mais utilizada no controle automático de processos industriais, sua função é manter o valor de uma variável de um processo no valor desejado.
Por exemplo, manter a temperatura de um forno de tratamento térmico alimentado a óleo diesel onde o controlador PID controla a temperatura ajustando continuamente a abertura da válvula de óleo diesel a partir das leituras do sensor de temperatura, compensando automaticamente as perturbações no processo causadas, por exemplo, pela abertura da porta do forno para a carga e descarga das peças.
A função PID compara o valor desejado (SV) da variável temperatura com o seu valor atual (PV) e se existir uma diferença entre eles, chamada de erro (E), a saída do controlador (MV) vai agir sobre o atuador da válvula de controle do óleo para corrigir este erro.

O controlador PID consiste de 3 ações de controle: Proporcional, Integral e Derivativa que somadas vão determinar o valor final da saída de controle MV normalmente expresso como um valor entre 0 e 100% que correspondente à posição do atuador totalmente fechado e totalmente aberto.
Um outro bom exemplo de controle PID é o sistema de piloto automático (cruise control), onde o motorista pode escolher a velocidade desejada, tirar o pé do acelerador e deixar para o sistema a tarefa de controlar o acelerador para manter a velocidade do carro.
Nos próximos tópicos vamos explicar as 3 ações de controle que compõem o controle PID e utilizaremos o exemplo do piloto automático para mostrar a contribuição de cada uma delas sobre o atuador que controla o acelerador do carro.
O Controle Proporcional (P)
O controle proporcional provoca uma ação sobre a saída de controle (MV) que é diretamente proporcional ao valor do erro, sendo que o erro é a diferença entre SV e PV.
Esta relação entre o erro e a saída é expressa pela equação:
MV(p) = Kp x (SV – PV) ou MV(p) = Kp x Erro
Qualquer variação no erro provoca uma reação instantânea na saída MV que é proporcional aos valores do erro e do ganho, assim, ao ajustarmos o ganho Kp podemos modificar a intensidade da resposta do sistema ao erro.
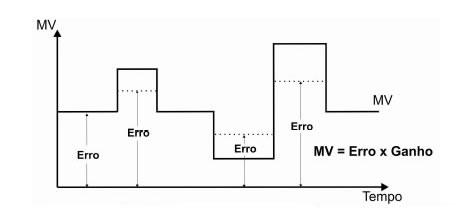
Utilizando o exemplo do piloto automático vamos analisar o comportamento da ação proporcional(P):
Se o carro já está na velocidade desejada o erro é zero, pois SV = PV, e se o erro é zero, a saída MV do controlador também é zero, pois Kp x 0 = 0, não importando o valor do ganho Kp.
Se a saída de controle MV é zero o atuador fecha o acelerador e coloca o carro em marcha lenta, e, se o carro está em marcha lenta a única possibilidade de continuar mantendo a velocidade desejada é estar andando num declive.
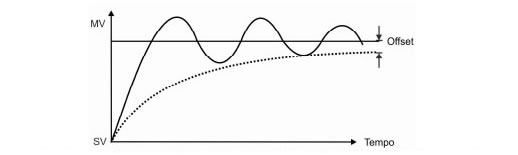
Este exemplo mostra a deficiência da ação proporcional: se o erro fica = 0 a saída MV também fica = 0, o que torna impossível manter o valor desejado. Então este tipo de controle exige que exista sempre uma diferença (erro) entre o valor desejado (SV) e o valor atual (PV) para que exista uma saída de controle (MV) com valor suficiente para manter o acelerador aberto.
Esta diferença (erro) num sistema estabilizado é chamada Offset que é justamente o erro cujo valor multiplicado pelo ganho fornece uma saída MV suficiente para manter a variável PV num valor constante e próximo ao valor desejado SV.
Nos controladores de processos proporcionais existe um ajuste chamado bias que acrescenta ao SV original o desvio necessário para o sistema compensar o offset e manter o valor SV desejado. Assim SV = SV(o) + bias
No controle proporcional o fator mais importante é o ajuste do ganho Kp que se for muito elevado vai provocar reações muito violentas de MV às variações do erro que podem causar oscilações e impossibilitar um controle estável, por outro lado se Kp for muito pequeno as oscilações não ocorrerão, mas o processo vai demorar a estabilizar e vai apresentar um grande offset.
Em muitos controladores PID o ganho Kp é chamado de banda proporcional (PB) que é o valor percentual do erro que provoca uma variação de 100% em MV. Por exemplo, se PB = 1, um erro de 1% de PV em relação a SV faz a saída MV atingir o valor máximo de 100% (ganho = 100), se PB = 2 , o erro precisará chegar a 2% para que a saída atinja 100% (ganho = 50).
O Controle Integral (I)
O controle integral age sobre a saída de controle MV enquanto existir um erro (offset) e sua contribuição cresce com o passar do tempo visando eliminar este offset.
No controle proporcional quando o erro é pequeno o valor da saída MV(p) é insuficiente para eliminar o offset, mas a ação do controle integral pode eliminar o offset mesmo com um erro muito pequeno, pois sua ação cresce com o tempo aumentando continuamente o valor da saída MV(i) enquanto existir um erro.
O tempo que o controlador I precisa ficar agindo para que sua saída atinja o mesmo valor proporcionado pela saída do controlador P a um determinado erro é chamado de Ti, que é o tempo em que MV(i) repete o valor de MV(p), por isso em muitos controladores Ti é expresso em repetições por minuto.
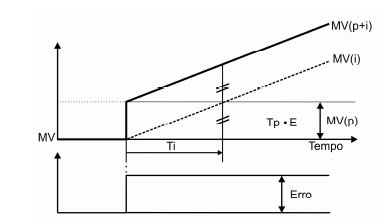
Resposta do controle PI a um erro mostrando que após o tempo (Ti) a saída MV(i) alcança o valor de MV(p).
A ação do controlador I sobre MV é expressa pela equação:
MV(i) = Kp/Ti ∫ E.dt onde: o símbolo ∫ representa a integral do erro em função do tempo
O controlador I a cada intervalo de tempo multiplica o erro atual por Kp/Ti e acumula o resultado em MV(i) e a cada novo intervalo um novo valor é calculado e somado ao resultado anterior, assim o valor de MV(i) continua a crescer enquanto existir um erro diferente de zero.
A ação integral I só existe associada ao controle P formando o controle PI (P+I) cuja expressão é
MV = MV(p) + MV(i)
Onde MV(p)= Kp x E (ação proporcional) e MV(i)= Kp/Ti ∫ E.dt (ação integral)
Podemos aumentar ou diminuir a ação integral ajustando o tempo de integração (Ti). Assim, se aumentarmos (Ti) estaremos enfraquecendo a sua ação para a saída MV, e se diminuirmos Ti estaremos aumentando a sua contribuição para a saída, mas se o aumentarmos muito podemos fazer o sistema entrar em oscilação impossibilitando um controle estável.
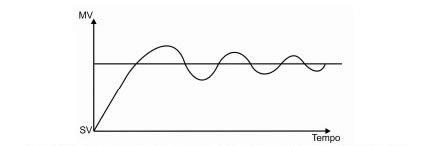
Novamente utilizando o exemplo do piloto automático vamos analisar o comportamento da ação integral I associada ao controle P: controle PI (P+I).
Conforme já vimos no exemplo anterior, se o carro está numa velocidade constante devido a ação do controle puramente P então deve existir uma diferença(erro) entre a velocidade desejada (SV) e o valor real(PV) chamada de offset que multiplicada pelo ganho Kp está agindo sobre o atuador do acelerador para mantê-lo na abertura necessária para a manutenção da velocidade atual.
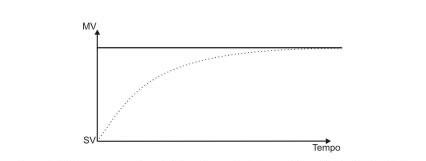
A ação combinada das saídas MV(p) + MV(i) compõe a saída MV do piloto automático que vai aumentando gradativamente a aceleração e reduzindo o erro na velocidade até zerá-lo totalmente, eliminando o offset.
O exemplo demonstra a superioridade do controle PI sobre o puramente proporcional(P), pois após um intervalo de tempo o erro permanente(offset) é eliminado.
O Controle Derivativo (D)
O controle derivativo age quando existe uma variação no erro provocando uma reação na saída MV que é proporcional a velocidade da variação do erro e não a sua magnitude, sua ação só existe associada ao controle P e enquanto o erro permanece constante a sua contribuição para a saída MV é igual a zero.
Se após uma perturbação no processo o erro dobrar de valor a saída proporcional MV(p) também dobrará seu valor. Na ação derivativa, no entanto, mesmo uma pequena variação no erro, se ocorrer num curto espaço de tempo, provoca uma grande reação na saída derivativa MV(d).
Assim podemos dizer que a ação derivativa antecipa a reação da ação proporcional, pois pode produzir o mesmo resultado na saída MV num tempo muito menor.
Chamamos de Td o tempo que a saída proporcional MV(p) leva para alcançar o mesmo valor produzido por MV(d) a uma variação no erro, ou seja, podemos dizer que MV(d) antecipa a ação MV(p) pelo tempo Td.
A unidade mais utilizada nos controladores para designar este tempo é expressá-lo em minutos.
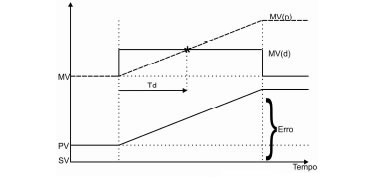
A ação do controlador D sobre MV é expressa pela equação:
MV(d) = Kp x Td dE/dt
onde dE/dt é a função matemática da derivada do erro em relação ao tempo.
Utilizando ainda o exemplo do piloto automático vamos analisar o comportamento da ação derivativa D associada ao controle P: controle PD.
O carro está numa velocidade constante controlada pela saída MV(p) e encontra um pequeno aclive seguido por um trecho plano, imediatamente a velocidade começa a diminuir aumentando o erro de velocidade(offset) e provocando um aumento proporcional na saída MV(p), mas esta reação está atrasada, pois só terá um efeito efetivo na aceleração quando o erro já for significativo.
O controle derivativo, no entanto, vai agir imediatamente com toda a sua intensidade no instante em que o erro aumentar, no início do aclive. Esta reação vai evitar que a velocidade se altere significativamente e vai desaparecer quando o carro atingir o trecho plano e o erro ficar novamente estável (offset constante), ficando então o controle apenas a cargo da saída MV(p).
Este exemplo demonstra o efeito estabilizador da ação derivativa devido a antecipação da ação corretiva.
O Controle Proporcional + Integral + Derivativo: PID
A combinação das ações individuais das 3 saídas MV(p), MV(i) e MV(d) descritas anteriormente compõe o controle PID:
MV = MV(p) + MV(i) + MV(d)
Neste tipo de controle combinamos a ação proporcional ao erro de MV (proporcional) com a capacidade de eliminação do offset da ação MV (integral) e ainda adicionamos o efeito estabilizador da ação antecipativa da MV (derivativa), o valor final resultante MV será o valor transferido para o atuador do processo.
É assim que funciona o piloto automático (cruise control) dos automóveis e a maioria dos controladores de processos automáticos nas mais variadas áreas: industrial, aeronáutica, naval, militar, etc.
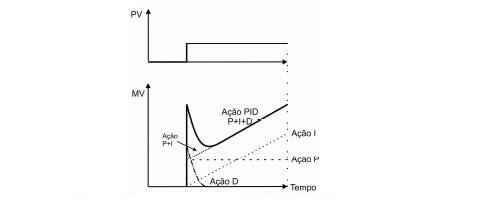
O gráfico acima apresenta a resposta do controlador PID ao tipo mais simples de erro(degrau) e como podemos ver, a resposta do controlador é bastante complexa e muito difícil de ser compreendida.
Para utilizar um controlador PID o usuário precisa ajustar o ganho das 3 ações Kp, Ti e Td, fazendo um processo que chamamos de sintonia do controlador PID.
Estes ajustes, bastante difíceis, são normalmente feitos empiricamente pelos instrumentistas baseados na sua experiência e intuição, mas também podem ser feitos através de métodos de ajuste como o Ziegler-Nichols que combinam modelos matemáticos com testes práticos da resposta do processo.
Felizmente, os controladores de processos atualmente disponíveis possuem o recurso da auto-sintonia (auto-tuning) que automaticamente calcula e ajusta o valor do ganho das 3 ações, permitindo que mesmo usuários com poucos conhecimentos possam utilizar satisfatoriamente esta poderosa ferramenta de controle.





